
We have just spent several pages exploring how to turn perfectly reasonable data into garbage. If not garbage then into a number that is uniform randomly distributed across some range. This seems a useless process, even if you can do it fast -- here's a way to use it.
Let's say you want to store the names of all the students at the University of Auckland and their addresses and phone numbers on your computer. So list them all and store them. Easy!
Now you want to search for them. So you give someone's name and your program goes sequentially through the names trying to match it. When it finds the matching name it prints out the name, address, and phone number. This is a slow process, it is taking minutes to do each one. Could you make it faster?
First hash the names by using the name as the key using any of our three hash functions, ask it to produce a number between 0 and 90, e.g. a hash table size of 91. This gives a small integer number, this is invariant, the hash function will produce that same integer number whenever that particular key is hashed. Another key, one with only a single character, perhaps only a single bit changed, will give some completely new number. Make 91 independent bins, one bin for each hash value. Each bin will have in it only those names whose keys also that have that hash value. Now to look up something do the following: hash the name and look for it only in its proper hash bin. Since the probability that any key will land in any given bin is equal, the names will be distributed in a uniform random way across the bins. Thus by doing the small hashing calculation the search can be done in about 1/91 of the time. If it took a couple of minutes before, it will take about a second now.
Thus the idea of hashing for data retrieval is to divide the search into a smaller search that can be done faster. How fast can we go? Clearly getting the name in one probe should be possible, what is the cost?
Let's try the obvious strategy. If we had the same number of hash bins as we have names then we should be able to get at something in close to one try. Well, that's not really true. With the table the same size as the data the probability of two keys falling in the same bin begins to get high. About a third of the names will have the same bin value. So in this 1 record for 1 bin case you will have to look through about 1.5 names and about 37 percent of your bins will be empty, that is wasted space. To get data in a single access it requires a density of about 0.03 (found by looking at Graph G1) or about 30 times the number of bins as records; this is probably not worth the wasted space in exchange for a minor increase in time (at a load factor of one searching only requires looking at an extra record about half the time).
Think about the bins collected together into an array or table, the index into the table is the hash value; you see where the name hash table comes from. Call the number of keys divided by the number of bins the load factor, or the table density. If the load factor is 1.0 then there are just as many keys as bins. If its 2.0 then there are twice as many keys as bins. If its less than one then there are more bins than keys.
Unlike any other data structure for retrieval hashing provides such a good retrieval method that the question is not how fast can I get to my data, but rather how fast do I want to get at my data. The cost of faster access is more memory. So to use hashing you need to think about how much time and space you are willing to allocate to getting data.
The graph G1 shows the load factor of the hash table along the bottom of the graph, the vertical axis gives the number of keys that will have to be looked at in the hash bin to find the key you want. It gives one curve if your search is going to be successful, and one if the search is going to be unsuccessful. The remaining curve is the best possible access if no randomization were done and each key ended up its own bin or in a minimal number of bins if the load factor is greater than 1.0.

| Graph G1. Search Probes of Ordered Bin Chains × Load Factor |
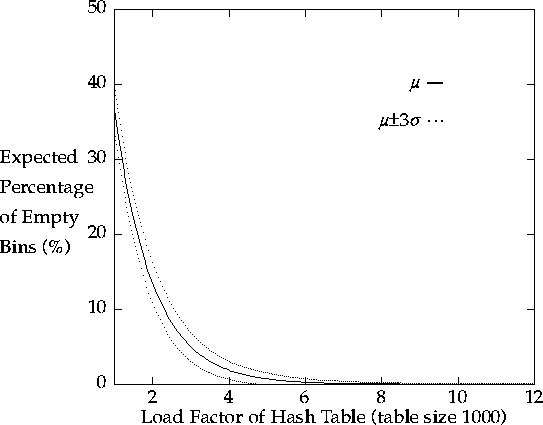
| Graph G2. Empty Bin Percentage in Hash Table × Load Factor |
The formula for the average successful and unsuccessful ordered search is:
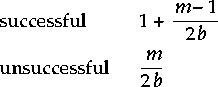
From graph G1 you can see that as the density goes up so does the
amount of work needed for retrieving a key.
What the graph doesn't show is how much space is required for the
search.
Graph G2 shows the amount of unused space required for a given load
factor.
If n keys are uniformly hashed into m bins, assume bins are
identical, the probability of any particular bin to be empty
(i.e. no key falls into it) is 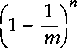 .
Also assume that both m and n are large but the load factor
defined by
.
Also assume that both m and n are large but the load factor
defined by 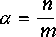 , is small, then this probability will become
, is small, then this probability will become
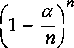 , that in turn can be
approximated by
, that in turn can be
approximated by 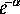 for large n.
for large n.
From these graphs (or formulas) you can design a retrieval strategy
that will work for your program, balancing unused space against access time.
Since you can chose your time performance, there is nothing that can beat
this method of retrieval.
It does require that you know the approximate size of data you are going
to process.
But the method is forgiving of small to moderate errors in the estimate
of the amount of data.
Large errors in the estimate of the amount of data will require rethinking
the sizes of things but will not require a change of algorithm.