
Binary arithmetic is said to be base 2 arithmetic because its digits represent powers of 2. Other bases for arithmetic are possible, for example base 8, which has the digits 0 to 7, and has successive powers of 8 in a number. Base 8 is called octal, and it is a `nice' base because numbers can be converted easily between octal and binary. Another nice base is hexadecimal, base 16.
First note the relationship between the values between 0 and 16 in hexadecimal, decimal, octal, and binary.

Any binary number can be converted to octal by breaking up the number
into three bit segments starting from the right of the number,
each segment should be rewritten as the corresponding octal digit.
Likewise any octal number can be represented in binary by
just replacing the octal digits by the binary bit representation
of the corresponding digit.
Numbers computed in octal will yield the same values as numbers computed
in decimal or binary, so what base one chooses to do arithmetic in is
not significant.
If one cares about the bit representation of a number then doing arithmetic
in a bit compatible base, one where the base is a power of 2, is most
convenient because it provides an easy way to see the bit representation
behind the number.
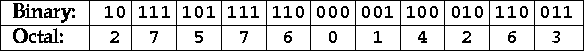
The figure shows that to convert from binary to octal one groups bits three at a time starting at the right (or units position), each group of three bits is rewritten as its octal equivalent. What happens if you start from the wrong end? To go from octal to binary write the binary representation of each octal digit in the same relative position. If you get too many binary digits for the machine representation then truncate zeros from the left end of the number. If you have to leave out a one something is probably wrong, check out what you are doing.
One can build octal addition, subtraction, and multiplication tables the same way one can build binary and decimal ones. The arithmetic rules are the same only the tables differ.
In hexadecimal numbers 16 digits are needed. Each digit maps to four binary bits. The usual convention is to use the letters A, B, C, D, E, and F for the additional digits, which have the values 10, 11, 12, 13, 14, and 15. These equivalences were used in the table above to represent the hexadecimal numbers. To do arithmetic in hexadecimal it is necessary to memorize the value of each of these digits.
Conversion between binary and hexadecimal is only a matter of rewriting the groups of four binary digits in their more compact hexadecimal form. It is done the same way as was shown for octal conversions. Conversion the other way expands the hexadecimal digit by replacing it with the corresponding set of four binary digits. Again arithmetic tables can be built for hexadecimal numbers.
Hex numbers are frequently used because they provide a compact representation of data in modern computers. In hex, 2 hex digits represent one byte, 4 hex digits represent a 16-bit number and exactly 8 hex digits represent a 32-bit number. These are the most common forms of data in the current generation of machines.
Word sizes in computers, e.g. the size of an integer or small real, tend to be a power of 2 in modern machines, the most common being 16 and 32. As time progresses arithmetic word sizes have gotten larger, in part because of the dramatic cost reduction in hardware, which allows machines to have bigger numbers at roughly the same cost. It would be possible to have the next generation of machine use 48 bits, if there were a good technological reason, but 64 bit integers seems to be where computer designers and manufacturers are going.
It is convenient if the base one uses to describe bits in a machine divides evenly into the size of a word. Then each digit in the base is completely used, and extra zero bits are not needed to fill out the word to a multiple of the base bit size. For example if you use octal to describe an 8-bit byte, it takes three digits (e.g. Dec 255 = Hex ff = Oct 377, but you have to remember that the first digit of the octal represents only two bits).
Base 32 (5 bits) or 64 (6 bits) are other possible binary compatible bases. Neither five bits nor six bits divides evenly into most powers of two, so there is usually some added bits to be appended to make the number a multiple of five or six to do conversion, just like the octal example. Besides to do arithmetic one needs to remember the value of each of the 32 or 64 digits. Alternatively one could memorize the large arithmetic tables associated with these bases. Both of these properties make using base 32 or 64 difficult. So your future holds octal or hexadecimal as the representation of binary numbers in computers. You might as well get used to them.
These general base arithmetic and number concepts should not be new to you;
they should have been covered in your secondary school education.
If you are not familiar with other bases you should make yourself
comfortable with general arithmetic by doing exercises in octal,
hexadecimal, trinary (base 3), and maybe do a little base 13 stuff,
the extra digits in base 13 could be B=10, U=11, and Z=12.
Check results by hand converting numbers into decimal!
It should not come as a surprise if you are expected to do arithmetic
in some arbitrary base on the final exam.