The philosopher George Boole (1815-1864) invented a two valued formal logical algebra, often called Boolean arithmetic, or Boolean logic. This is the primary method used to make logical decisions within most programming languages. Most computers also have the Boolean operations as basic machine instructions.
In Boole's system F represents false and T represents true. We can view these as equally likely alternatives and assign bit values to them. Let 0 be false and 1 be true.
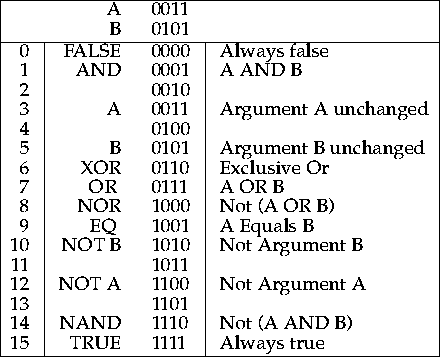
How many possible functions of two Boolean variables are there? There are sixteen, but many are not particularly useful. If A is the first variable and B the second variable then the table below shows all the possible functions.

Most of these functions are not particularly useful. The two functions FALSE(0) and TRUE(15) are independent of both variables. The four functions A(3), B(5), NOT A(12), and NOT B(10), are really functions of only one variable because the output is independent of the other variable. The four unnamed functions are only true under one specific set of circumstances.
So 10 functions of the 16 possible are not useful. Of the remaining 6 functions NAND, NOR, and EQ are just the NOT of AND, OR, and XOR. So there are really only three functions of interest. The negative functions NAND, NOR, and XOR are often used in hardware design, because they correctly model the operation of fundamental electronic components. However most programming languages use Boolean conditional operations using NOT, AND, OR, and XOR.
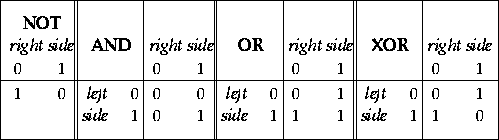
The NOT operation works on a single bit and yields the opposite value. AND gives true if both operands are true and false otherwise. OR gives true if either or both operands are true, and gives false only if both operands are false.
An important Boolean function is exclusive-or or XOR. This function is sometimes called Half-ADD because it represents an add with the carry forgotten; it also sometimes called NotEqual because it represents a true when both operands are different, and a false when they are the same. XOR will also invert like NOT if one of its arguments is the constant true. A useful set of properties of XOR that you should remember is:

These Boolean functions can be represented as tables,
just like the arithmetic tables in the last
section NOT, AND, OR, and XOR take the following form:
Boolean logic does not directing translate the English meaning of the words `and' and `or'; don't try to reason with them that way. In English one can build a set with either `and' or `or' and everyone will understand you, in Boolean logic only OR will do to build up a set. For example you might say `Bob' and `Bill' and `Judy' and I are going to the beach. That builds a set with the English `and'. But you might equally well say I could `go to bed' or `watch television' or `study my CS105', again building a set with the English `or'. The difference in English is the `or' implies you are going to choose from among the members, where the `and' implies them all; but they are both set builders. The English `and' and `or' are often used in daily language in the logical sense as well. This overuse in English makes the logical operators somewhat confusing and you have to take care that you use the formal Boolean meaning when you try to understand a program. Your native intuition about the meaning of a complex Boolean expression will often be wrong: take care!
Boolean logic is sometimes called Boolean algebra because there is a strong relationship between this logic and arithmetic. Think of OR as `+', AND as `×', true as 1, and false as 0!
The same rules of algebra work on Boolean expressions.
The Boolean operations AND and OR are commutative and associative
in the same way the × and + are.
For example the distributive law of algebra is
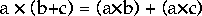
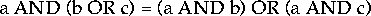
So you might think that it shouldn't take much to get used to Boolean
algebra and make it work for you.
Boolean expression are surprisingly unintuitive and
complex Boolean expressions are often difficult to understand.
On occasions you will find them even more difficult to write
so they do what you want.
However in computers they are universal,
they are the essential logic base from the bottom of the machine
to the most high-level programming language.
As a computer literate person you will just have to learn to suffer along in
Boolean logic. Practice does help.
One law that helps simplify Boolean expressions (and makes them easier
to understand) is called De Morgan's rule.
It says one can factor NOT into an expression by taking all
the ANDs and changing them to ORs, and all the ORs and changing
them to ANDs, and at the same time negating all the arguments.
So:
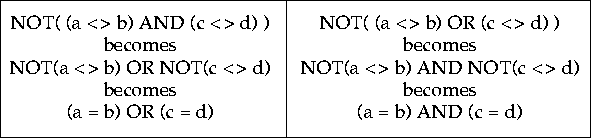
If you do forget it and show you don't understand
it on some future exam, any time in the next three years, the
Computer Studies Department has a policy of automatically transferring
you to the Arts Faculty and retroactively failing you for all courses
taken in computer studies.
Most programming languages (like Pascal) use logical values for flow-of-control, Boolean expressions provide the logic tests of conditional and looping statements.
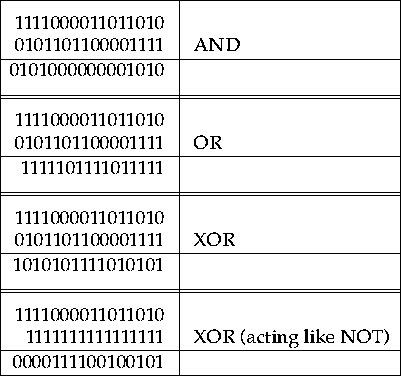
These Boolean operations can also be used as bit manipulation operations that have an entirely different flavor from Boolean logic. Pascal underplays this bit-wise use of logical operators on integers, where the AND, OR, and XOR operate on corresponding bits in two integers. These bit-wise functions are however some of the most powerful tools available in the machine. For example, an XOR of two integer variables can be seen as hiding the the two argument variables in another random value, but if you know either argument then you can get the other. Most computers supply these logical operations as hardware primitives that work on computer words bit-wise. Thus if one has two Pascal 16-bit integers, which are stored in machine words, then 16 ANDs can be done in parallel between corresponding bits of the two integer values used in the operation. So here are some examples of combining two 16-bit values with various boolean operations.
Using these bit-wise operations one can manipulate patterns of bits. For example to extract a portion of a number one might `mask' the bits one wants using an AND operation. For example if one had a 16-bit number and wanted the value of the five bits starting at binary point 3 one could use the 16-bit mask: 0000000011111000. If the mask and the number are ANDed together the result will have 1 bits only where there were 1 bits in the mask and the number. A shift of three binary places to the right will provide this portion of the number as an integer.
In a similar way certain portions of a number can be changed. For example if one had a 16-bit number and wanted to insert the number 10010 into it at binary point 3 one could use the 16-bit mask: 1111111100000111. ANDing the 16-bit number and the mask will zero the five bits, then the 10010000, 10010 shifted left 3 bits, can be ORed or XORed with the number inserting the new information into the number. A portion of a number used in this way is usually called a field.
Other computer operations that work on a series of bits are the shift operations.
These operations exist in Think Pascal as the bit operations:

Logical shift operations which move bits right, left, and circularly are also commonly provided in the hardware of computers. Logical shift operations insert zeros from the right or left; the circular shifts take whatever bits drop out of one end of the word and put them into the other end.
In many computers there are arithmetic shifts that `understand' the function
of the sign bit, so that a right shift copies the sign bit in the
bit position to the right and a left shift doesn't change it.
