To what extent does the mathematical model of randomness correspond the real world? A mathematician takes it on faith that flips of coins and Lotto draws behave as a mathematical model would predict. However that is a belief based on faith, and it is not a provable thing. That is unless one uses the first, more concrete, process oriented definition and agree that the Lotto machine implements that ideal mathematical draw from a well mixed urn. The more abstract the mathematical definition the more faith is needed that it models the real world.
What makes a coin flip, or a Lotto draw, random in the real world is that there are so many varied immeasurable forces working on the coin, or Lotto balls, that the outcome is uncertain, certainly unpredictable, and therefore random.
Does a mathematician's faith really apply to our finite world? Or is mathematical randomness only true as a mathematical abstraction? Is this the statistical equivalent to Euclid's flat earth? Not many people really believe the mathematical definition of randomness; instead, they show by their actions, that they believe that every random choice has a past. Where is the truth?
Denying the mathematical assumption that numbers are independent and
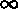-distributed in a random sequence is called
by mathematicians the gambler's fallacy.
The gambler's fallacy is the belief that a sequence of `random numbers'
will correct itself to become more `average' or `random'.
Thus if one number has not come up for awhile it has a higher likelihood
of coming up next.
This common gambler's belief explains why there are lists of how many times given numbers have come up in the NZ Lotto posted in Lotto stores. In mathematical random sequences the past is never a guide to the future, no matter how unbalanced it is, this is true by the mathematical definition of randomness. I suppose that is for you to decide. If you use the numbers on the Lotto chart as a guide to gambling then you believe with the masses, if you bet on the numbers: 1, 2, 4, 8, 16, 32 then you are an optimist and probably a computer scientist.
In this practical world you might think that you could turn scientist and test for randomness. Statistical tests of `random' sequences may show that there is some probability that a sequence is inconsistent with the hypothesis of randomness. But statistics don't `prove' randomness.
This is like going to court, you don't get proved innocent, you get
judged as not guilty beyond a reasonable doubt.
You could still be guilty, maybe you are even `probably guilty',
but there is not enough proof to punish you.
The statistical tests show a suspected lack of randomness, making you almost
sure that the sequence is non-random:
you choose some percent level of confidence and accept the sequence or reject
it.
But in a mathematical random sequence, which is the assumption
underlying a statistical test, all finite length strings of numbers are
equi-probable, so it still might be the output of a random source,
no matter how unlikely.
Statistical testing doesn't tell us anything for sure,
it only quantifies the probability that some sequence is not random.
This tells little about the generator, since the next sequence out of
the generator may pass the test with flying colors.