Library Hash Functions

In 1989, Bruce McKenzie and his co-workers at the University of Canterbury, Christchurch, New Zealand, developed several methods for evaluating hash functions and by studying and measuring many hash functions they empirically discovered odd behavioral properties of most of the commonly used hash functions [mckenzie90].

The performance problems exposed by this hash function testing showed that the average cost of searching can range over several orders of magnitude using the same hash function varying only the output range. This seemed to be directly attributable to the sensitivity of the result on the modulus applied at the end of the hashing operation. This property makes most functions unacceptable as a library hash function because they need to be tested for the specific range over which output is expected.

CBUhash

In the McKenzie paper the authors conclude that for hashing program identifiers, the following linear hash function, presented here in its simplest form, is a good hash function. ^¹

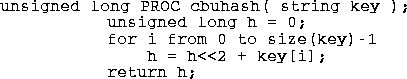
This function is named cbuhash for CanterBury University, in Christchurch, New Zealand, where it was developed. It works by using random variations in low-order bits of the key characters to create noise which masks the high order bits of the characters. To finish the mixing the resulting hash value must be divided by an odd number and the remainder used as the operational hash. This means that one must always have a odd number of bins in the hash table. This hash function works particularly badly for hash tables whose size is a integral power of two.

This cbuhash hash function has the advantage that it is fast to compute, it seems to work well for an ASCII character string domain, and it has a broad range for which it works. This algorithm and variations of it have been used in modern programs, for example the Revision Control System [rcs91] uses the same algorithm but with an exclusive-or replacing the plus in the computation of the hash.

PKPhash

In 1990, Peter K. Pearson published a random walk hash algorithm which produced integers from 0 to 255. He claimed this algorithm worked well for text strings (with 8-bit bytes). (See [pearson90].) Pearson uses a compile time static table, ptab, of unsigned byte values [0-255] that have been randomly permuted which he uses to introduce noise into the key. The Pearson algorithm is:

A defect in this hash algorithm is that for hash ranges greater than 0-255 pkphash becomes more costly. In fact for a 64-bit range it will cost roughly 7 times more to compute than for a range of 0-255. With the inner loop expanded for efficiency, the algorithm is as follows: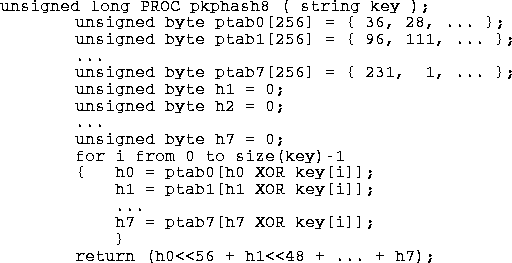

BUZhash

At about the same time Pearson's hash function was published I was looking for a hash function. Reading his algorithm I was sure that a new algorithm could be designed that would compute a large hash value more cheaply. At the same time a friend suggested I look at the McKenzie article in Software Practice and Experience. Using McKenzie's techniques for measurement I found a hash algorithm that requires the use of a random table 256 words large, where a word is defined as the maximum data size that an XOR function can be applied to easily in the programming language. Depending on the programming language and the machine this word size can assume different values: using C on a modern PC this is 32 bits, in PL/I on an IBM 360 this is 2048 bits, and in Java on a byte-code machine it is 64 bits. If you assume unsigned long is 64-bits, and strings have 8-bit bytes then a library hash function suitable for Java might look like the following:

The cshift is a circular shift (or rotation), that can be applied in either direction. The rtab table is a compile time constant array that should have the property that in every bit position vertically in the table, there should be exactly 128 zeros and 128 ones. This makes the probability of change in all the hash bit positions ½, giving a uniform random distribution. The Java buzhash is designed to work for keys shorter than 65 characters; this does not limit programs much because rarely are keys encountered that are greater than 64 characters long.

Other Hash Functions

A hash function based on a pseudo-random number generator has been around for several years. I have not been able to trace its source to a publication. It works on a linear congruential random number generator, but any generator that provides a satisfactory random distribution modified to fold in the bytes of the key should also work. Here is the code for a 64-bit version of this function; here it makes no difference what byte size comes from the string.

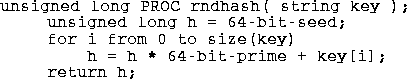
Note that this function tends to be a bit slower than pkphash and buzhash since it requires one multiply for every byte of key. To really use this function a good value for the multiplier must be found and the resulting hash function tested. As far as I know this has not been done for a 64-bit word.

The academic cryptographic community has produced several secure hash functions that distribute keys randomly [pieprzyk93], but for general retrieval use cryptographic hash functions tend to work too slowly to satisfy most users.

Footnotes:

^¹ This and other functions in this paper are represented in SAL, the Sketchy Algorithmic Language. SAL leaves its definition and precise meaning up to your imagination. This is done to avoid language quirks and provide a clean representation of the ideas. For example, to show these algorithms in Java the code would have to deal with signed numbers when the algorithm is most naturally expressed in unsigned long integers. Dealing with the wrong type tends to confuse rather than help understanding. Likewise to show them using C requires creating 64-bit integers from 32 bit ones, posing similar problems.